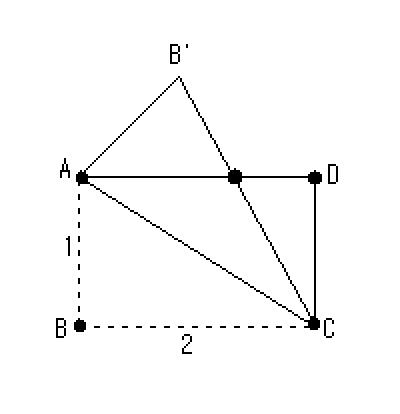
B`D의 길이는? 링크 http://todayhumor.co.kr/board/view.php?table=science&no=2407&page=1&keyfield=&keyword=&sb=&html=1 더 쉬운방법이 있을진 모르겠지만 일단 제가 푼 방법을 알려드릴게요 일단 전 두가지 공식을 쓸게요 1. 코사인제2법칙 2. cos(a-b)=cosxcosy + sinxsiny 삼각형 ABC에서 각A를φ, 각C를θ라고 둘게요 그럼 sinφ는2/√5 sinθ는 1/√5 cosφ는1/√5 cosθ는 2/√5 가 되겠죠 각 B`AC는φ가 되고, 각CAD는 θ니까 삼각형 B`AD를 그려보시면 각 B`AD는 φ-θ가 되죠 AB`길이는1, AD길이는 2 코사인제2법칙쓰면 X^2 = 1^2 + 2^2 - 2·1·2cos(φ-θ)가 되죠 여기서 cos(φ-θ) 이건 위에공식을 사용하여 계산하면되요 세부 계산은 생략할게요