- 가속운동(중력)과 공간의 휘어짐

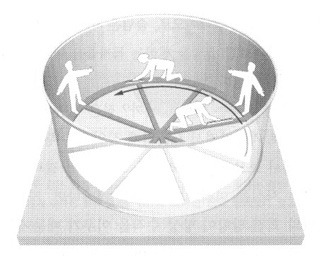
어린이 놀이터에 볼 수 있는 아래 그림과 같은 회전하는 원통모양의 놀이기구를 생각해보자.(미국에서는 이것을 '토네이도'라고 부른다고 한다.)

<그림2 토네이도>

우리가 중력을 느낀다는 것은 이 놀이기구 안에서 원심력을 느끼는 것과 차이가 없다. 만일, 눈을 가린채 무중력의 우주공간에서 이 놀이기구를 타고 있다면 지구의 중력을 느낄 때와 완전히 같은 느낌일 것이다. 우주정거장에서는 실제로 이런 방식으로 인공 중력을 만들어 내고 있다. 이 놀이기구에서 원의 중심으로부터 바깥 방향으로 가속운동이 작용하는 상황은 지구 위에서 중력의 영향을 받는 상황과 동일하게 취급할 수 있다.

어떤 사람이 놀이 기구 밖에서 기구의 크기를 측정한다고 가정해보자. 평범한 30cm자를 가지고 원판의 외곽을 따라 원의 둘레를 측정하고, 다시 원의 중심에서 가장자리까지 길이(반지름)를 측정하면 측정 결과는 학교에서 배운대로 '원의 둘레 = 2 x Pi x 반지름'의 공식에 맞는 결과가 나와야 한다.

그런데, 이번에는 회전하고 있는 놀이기구 안에서 30cm 자를 가지고 똑같이 원의 둘레와 반지름을 측정한다면 어떤 결과가 나올까? 기구가 회전하고 있으므로 원의 가장자리에 서있는 사람은 그림에서처럼 반시계 방향으로 운동을 하게 된다. 특수상대성이론에 따르면, 운동하는 물체는 길이가 짧아진다. 따라서 원의 둘레를 재는 사람이 가지고 있는 30cm자는 길이가 짧아졌을 것이고, 앞서 기구 밖에서 측정한 값보다 더 길게 측정되는 결과를 가져올 것이다. 반면, 반지름을 측정할 때는 측정하는 사람의 운동 방향과 수직을 이루기 때문에 자의 두께만 달라질 뿐 길이에는 변함이 없다. 따라서, 기구 밖에서 측정한 값과 똑같은 반지름 값을 얻게 된다. 그럼 이제, 회전하는 기구안에서 측정한 값을 가지고 앞의 공식에 다시 대입하면 어떻게 될까? 공식이 전혀 맞지 않다는 사실을 발견할 수 밖에 없다. 원의 둘레는 길어진 반면, 반지름은 같으므로...

이것은, 우리가 알고 있던 유클리드 기하학을 가속 운동 중인 물체에 그대로 적용할 수 없다는 것을 의미한다. 아인슈타인의 설명에 따르면, 고대의 유클리드 기하학은 평면에서만 성립한다. 가속운동을 하는 공간이나 아래의 그림처럼 휘어진 공간에서는 또 다른 기하학이 필요하다는 것이다.

<그림3 휘어진 공간의 예>

아인슈타인은 가속 운동을 한다는 것이 공간이 휘어진 것과 같은 효과를 낸다는 사실을 발견했다. 앞에서 예로든 회전운동에 관한 특별한 경우뿐만 아니라, 모든 가속 운동은 공간을 휘어지게 한다는 사실을 알아냈다.

- 엘러건트 유니버스 중

근데 책을 읽다가 이해 안되는 부분이 있는데요, "회전하는 원판의경우에 휘어진 공간을 4차원 시공간으로 확장시키면 곡률이 사라진다."는 무슨 의미일까요?