갑자기 생각난건데 x^n을 적분하는 법을 모르겠네요.
답은 알고 있지만 어떠한 과정으로 되는가.
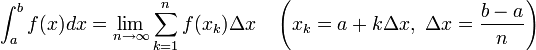
적분에 대한 기본 식은 이렇게만 나와있는데 이걸로는 정확히 감이 안와요. 양변의 넓이를 구해 비교해서 같다는건 할 수 있겠지만..
x의 적분이 1/2x^2으로 어떻게 변하는가를 이 방법으로 구하는건 모르겠네요.
위키에 가서 보니 조금 자세하게 나와있긴 한데 중간이 이해가 안되요.
처음부터 도함수와 원시함수의 미분을 같다고 가정하고 푸는것같은데;;
미적분학의 기본정리에 따라 적분은 미분의 역산이다. 즉, 함수 f(x)를 도함수로 하는 원시 함수 F(x)가 존재한다. 원시 함수를 구하는 과정을 부정적분(不定積分)이라한다. 이를 식으로 나타내면 다음과 같은 관계가 성립한다.[13]
예를 들어, f(x)=x 라고 하면 원시 함수 F(x)는 다음과 같이 생각하여 구할 수 있다.
이 때 도함수가 f(x)=x인 원시 함수 F(x)는 일반적인 다항식을 관계식으로 하는 함수이므로
의 형태가 됨을 알 수 있다. 따라서, 다항식의 도함수 계산법을 이용하면  가 되고,
가 되고,  는 임의의 상수가 된다. 즉,
는 임의의 상수가 된다. 즉,
 가 되고,
가 되고,  는 임의의 상수가 된다. 즉,
는 임의의 상수가 된다. 즉,다항식을 적분하니 다항식에 관계된다는건 알겠는데 x^2항이 어째서 추가해서 가정이 되는거죠?
그리고 다항식의 도함수 계산법이 뭐에여..; 저건 뭘한거에요;
기초 미적분학 책을 봐도 F(x)와 f(x)의 관계가 어떻게 연결되는지 자세히 설명해주는건 못찾겠던데 이 단순한 질문에 답좀 부탁드립니다 ㅜㅠ
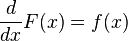
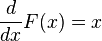
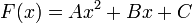



 글쓰기
글쓰기