-리만가설 part.1-
(글쓰기에 앞서 과연 제가 잘 설명 할 수있을지 확신이 안서네요ㅋㅋ 그래도 최선을 다해 보겠습니다!)
'리만 가설'은 1859년 천재적인 독일 수학자 리만(Geoorg Friedrich Bernhard Riemann,1826-1866)이 제시한 것으로, "2, 3, 5, 7 같은 소수들이 어떤 패턴을 지니고 있을까?"라는 질문으로 다음과 같습니다.
Hypothesis.
리만제타함수 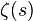 의 자명하지 않은 근 s의 실수부는 1/2이다.
의 자명하지 않은 근 s의 실수부는 1/2이다.
이 괴물같은 가설은 1859년 리만의 논문 <주어진 수보다 작은 소수의 개수에 관하여> 에서 언급했으나 그 논문의 중심적 목적은 소수의 개수에 관한 것이었기 때문에 가설의 증명을 시도하지는 않았습니다.
그러므로 리만가설 이야기는 소수의 개수부터 시작하겠습니다.
소수는 무한합니다. 유클리드가 매우 우아한 방법으로 증명했습니다. 혹여나 의심되는 분들을 위하여 소개하자면
Theorem. 소수집합은 무한집합이다.
proof.
P={p | p 는 소수} 이고 n(P)=n이라 하자.
q=p1*p2*...*pn + 1
이라면 모든 pi ∈ P에 대해서
q≡1 (mod pi)
이므로
gcd(q,pi)=1
즉, q는 합성수가 아니다. 하지만 q는 P의 원소가 아니므로 모순.
따라서 소수집합은 무한집합이다.
<Q.E.D>
소수는 무한하지만 에라토스테네스의 체를 이용하여 구해보면 나타나는 빈도는 숫자가 커질수록 적게 나타납니다. 연속해서 나타나는 경우도 있지만(이를 쌍둥이 소수라고 부르며 쌍둥이 소수가 무한한가를 묻는것이 쌍둥이소수 추측입니다.) 대체로 소수간의 간격이 멀어지는 걸로 보였습니다. 그래서 만든것이 소수계량함수입니다.
어떠한 소수계량함수(Prime-counting funct!on)는 주어진 양의 실수  에 대해 그 값보다 작거나 같은 소수의 개수를 세는 함수입니다. 보통
에 대해 그 값보다 작거나 같은 소수의 개수를 세는 함수입니다. 보통  로 표기하는데 원주율을 의미하는 그리스 문자
로 표기하는데 원주율을 의미하는 그리스 문자  와 아무런 관련이 없습니다.
와 아무런 관련이 없습니다.
예를들어볼까요?
10보다 작은 소수의 개수는 2,3,5,7로 4개가 있으므로 pi(10)=4.
100보다 작은 소수는 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97로 25개가 있으므로 pi(100)=25 입니다.
정수론에서 소수 개수의 증가속도는 매우 지대한 관심사였습니다. 60까지의 소수계량함수의 값을 나타내면 다음과 같습니다.
http://upload.wikimedia.org/wikipedia/commons/1/10/PrimePi.PNG
소수계량함수는 어떠한 다른 함수에 그사하는것처럼 보였고 18세기 말 가우스와 르장드르는 소수계량함수가 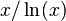 에 근접함을 추측했습니다. 즉,
에 근접함을 추측했습니다. 즉,
라고 생각했고, 이를 x=10^n인 표로 나타내면 다음과 같습니다.(li는 로그적분함수 입니다.)
| x | pi(x) | pi(x) − x / ln x | li(x) − pi(x) | x / pi(x) |
|---|---|---|---|---|
| 10 | 4 | −0.3 | 2.2 | 2.500 |
| 102 | 25 | 3.3 | 5.1 | 4.000 |
| 103 | 168 | 23 | 10 | 5.952 |
| 104 | 1,229 | 143 | 17 | 8.137 |
| 105 | 9,592 | 906 | 38 | 10.425 |
| 106 | 78,498 | 6,116 | 130 | 12.740 |
| 107 | 664,579 | 44,158 | 339 | 15.047 |
| 108 | 5,761,455 | 332,774 | 754 | 17.357 |
| 109 | 50,847,534 | 2,592,592 | 1,701 | 19.667 |
| 1010 | 455,052,511 | 20,758,029 | 3,104 | 21.975 |
| 1011 | 4,118,054,813 | 169,923,159 | 11,588 | 24.283 |
| 1012 | 37,607,912,018 | 1,416,705,193 | 38,263 | 26.590 |
| 1013 | 346,065,536,839 | 11,992,858,452 | 108,971 | 28.896 |
| 1014 | 3,204,941,750,802 | 102,838,308,636 | 314,890 | 31.202 |
| 1015 | 29,844,570,422,669 | 891,604,962,452 | 1,052,619 | 33.507 |
| 1016 | 279,238,341,033,925 | 7,804,289,844,393 | 3,214,632 | 35.812 |
| 1017 | 2,623,557,157,654,233 | 68,883,734,693,281 | 7,956,589 | 38.116 |
| 1018 | 24,739,954,287,740,860 | 612,483,070,893,536 | 21,949,555 | 40.420 |
| 1019 | 234,057,667,276,344,607 | 5,481,624,169,369,960 | 99,877,775 | 42.725 |
| 1020 | 2,220,819,602,560,918,840 | 49,347,193,044,659,701 | 222,744,644 | 45.028 |
| 1021 | 21,127,269,486,018,731,928 | 446,579,871,578,168,707 | 597,394,254 | 47.332 |
| 1022 | 201,467,286,689,315,906,290 | 4,060,704,006,019,620,994 | 1,932,355,208 | 49.636 |
| 1023 | 1,925,320,391,606,803,968,923 | 37,083,513,766,578,631,309 | 7,250,186,216 | 51.939 |
위의 표를보면 x=10^n에서 n이 증가할때마다 x/pi(x)의 값이 거의 일정하게 증가한다는 것을 알 수 있습니다. 즉 다음과 같은 근사식이 성립합니다.
Theorem. 소수정리(Prime Number Theorem, PNT)
두 함수  와
와  의 비가 x가 무한히 커질수록 1에 수렴한다.
의 비가 x가 무한히 커질수록 1에 수렴한다.
proof.
http://www.proofwiki.org/wiki/Prime_Number_Theorem
리만은 자신의 가설이 참일 경우 소수의 개수는 로그 적분 함수에 점근한다는 것을 보였습니다.
그래프로 나타내면 다음과 같습니다.
http://upload.wikimedia.org/wikipedia/commons/9/97/PrimeNumberTheorem.png
고독벽이 있었던 리만은 가설의 증거를 공개하지 않았고 1866년 리만이 사망하자 리만의 가정부가 집을 정리하면서 그의 연구자료를 불태워버려 그의 연구를 자세히 알 길이 없어졌습니다.
다음시간에는 디리클레 급수와 리만제타함수에 대해 알아보겠습니다.
[reference]
wikipedia
리만가설-존더비셔
[한줄요약: ]
]
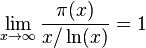
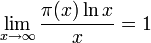



 글쓰기
글쓰기