http://bbs1.agora.media.daum.net/gaia/do/debate/read?bbsId=D115&articleId=2262592

 

 

매끈한 로지스틱 곡선이, 자연스러운 개표결과에 의한 누적득표수 곡선의 모습이 아니라는 저의 주장과 관련하여, ‘시사인’에서 이에 대한 교수들의 반론기사를 올렸으니, 여기에 답변을 해 달라는 네티즌들의 요구가 있어서, 그 기사를 뒤늦게 찾아보았습니다.

기사가 실려 있는 주소는 다음과 같고,

http://media.daum.net/economic/others/newsview?newsid=20130114091614188

기사 가운데, 로지스틱 곡선의 매끈함과 관련된 내용은 아래와 같습니다.

먼저, 기자가 다음과 같은 말을 했다.

"아래 그림은 아이디 '그루터기추억'이 지난해 12월25일 다음 아고라에 올린 '로지스틱곡선 의혹'을 대표하는 그림이다. 간단히 말해, 현실에서 찾아볼 수 없을 정도로 지나치게 매끈한 곡선이어서, 실제 개표 결과로 볼 수 없다는 것이 의혹의 요지다. 개표 결과를 인공적 함수에 따라 조작한 것 아니냐는 주장이 암묵적으로 깔려 있다."

"< 시사IN > 은 서울대 통계학과 장원철 교수와 통계 전문가인 박종혁 박사(고려대·산업공학)에게 검증을 의뢰했다. 두 사람이 보내온 답변을 정리하면 이렇다."

아래는 기사에 실려 있는, 교수들의 주장이다.

"그래프가 너무 매끈하다? 그래프의 y축의 범위는 0부터 1600만으로 보이는데, 개표방송에서는 거의 1분당 수치를 업데이트했다. 1분에 증가하는 득표수가 가장 많을 때 10만이라고 보아도, 그 차이는 그래프에서 눈으로 감지할 수 없어서, 매끈한 곡선처럼 보이는 게 당연하다.“

이런 교수들의 주장에 대하여, 시사인 기자는, 다음과 같은 말을 기사 끝에 첨부했다. “이 설명이 무조건 진실이라고만 단정할 수는 없다. 학계의 검증이 끝난 것도 아니다. 하지만 '논란'이 있다고 말하기에는, 전문가 그룹 내의 책임 있는 반론은 아직 존재하지 않는다. < 시사IN > 은 학계에서 실명을 걸고 이 문제에 의혹이 있다는 주장을 뒷받침해줄 전문가를 찾았으나 지금까지는 나오지 않았다.”

이 말은 교수들의 주장에 대하여 반론을 제기할 수 있는 다른 학자나 전문가를 아직 찾지 못했다는 말이다. 따라서 이 자리에서 제가 직접, 이에 대한 반론을 하고자 한다.

논란의 가장 핵심적인 요소는, 누적득표수를 나타내는 로지스틱형태의 곡선이 어떻게 전혀 굴곡이 없이 매끄러울 수 있는가 하는 점이다. 왜냐하면, 전혀 굴곡이 없는 매끄러운 곡선의 모습은 로지스틱 ‘함수에 의한 추정치’를 사용한 것이 아닌가 하는 의심을 충분히 불러일으킬 수 있기 때문이다.

먼저 교수들이 주장한 것은, 1분당 증가하는 득표수가 y축의 값에 비해서, 상대적으로 너무 작기 때문에, 1분당 득표수의 오르내림에 대한 차이를 그래프에서 눈으로 감지할 수가 없으므로, 그래프가 매끈한 곡선처럼 보인다는 것이다. 그러나 이 말은 항상 맞는 말이 아니다. 왜냐하면, 아무리 분당 득표수 증가가 1/160 또는 그 이상인 1/200의 비율로 증가한다고 하더라도, 얼마든지 그래프가 매끈하게 되지 않을 수 있기 때문이다.

다시 말해, 교수들이 주장하는 것처럼, 분당 최대 득표수( 10만 )가 y축의 최대값( 160만 )의 약 1/160에 불과하기 때문에, 누적득표수 그래프가 매끈하게 나타난 것이 결코 아니다. 그래프가 매끈하게 되고 안 되고는, 시간당 득표수 증가가 대체적으로 일정한 함수적인 모습으로 증가하느냐 아니냐에 달려 있는 것이다.

만약, 시간당 득표수 증가가 어떤 ‘함수적인 형태’로 변화된다면, 누적득표수 그래프는 매끈한 형태로 나오게 될 것 이다. 하지만 이와는 반대로, 시간당 득표수 증가가 어떤 함수적인 형태로 나타내기 어려운 모습으로 변화한다면, 누적득표수 그래프 역시 결코 매끈해지지 않는 것이다.

이제 이를 간단히 증명해 보겠다.

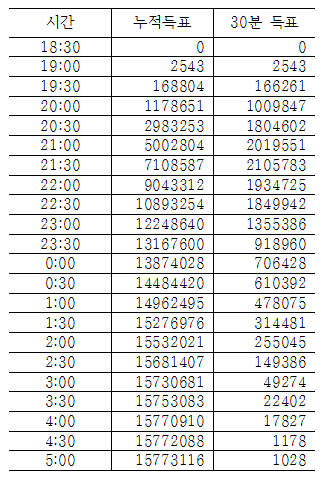
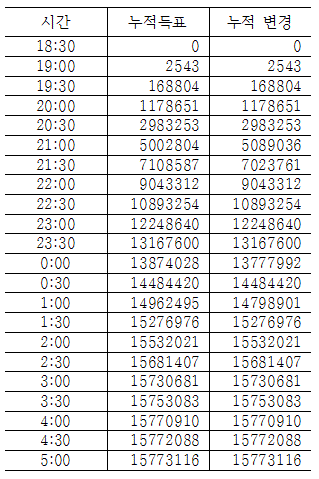
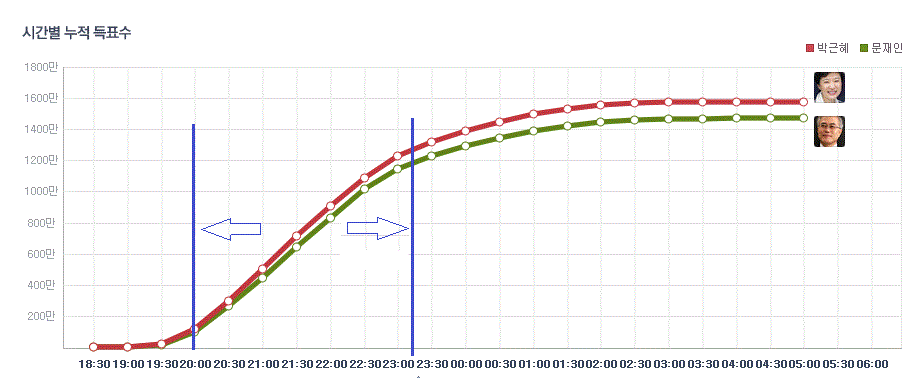
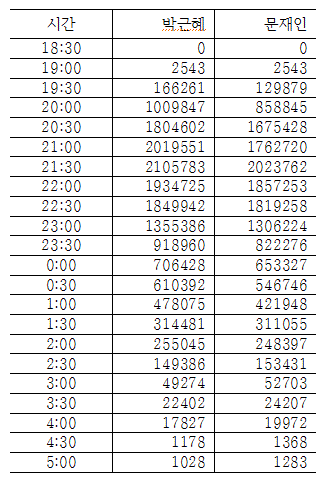
먼저 아래 표는 SBS에서 발표한 누적득표수 곡선을 나타내는, 박근혜 후보의 득표값 이다. 시간대별 누적득표수와 매 30분 간격의 단순득표수를 함께 나타냈다.

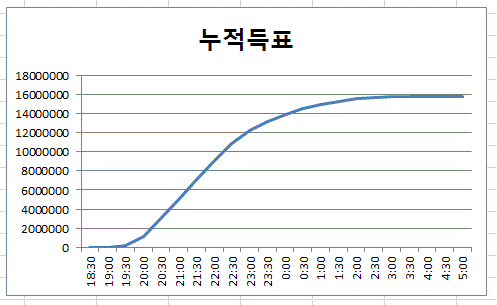
먼저 이들 표를 가지고, 누적득표수 곡선을 그려보면, SBS에서 발표한 것처럼 매끄러운 형태의 로지스틱 곡선이 된다.

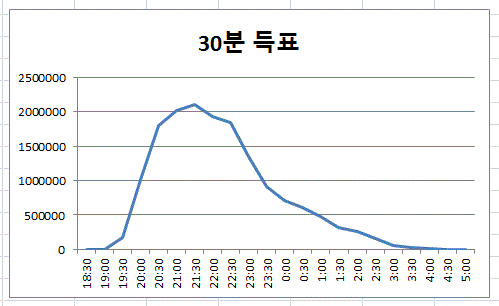
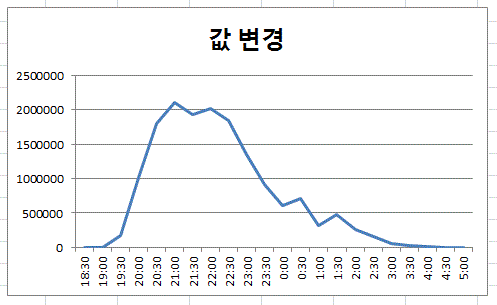
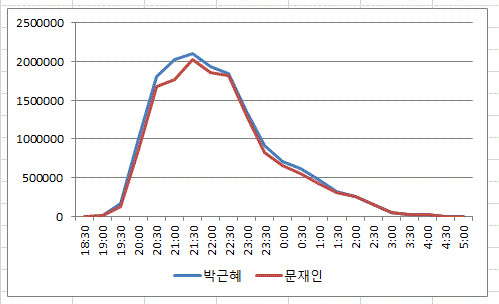
그리고 매 30분 간격의 단순득표수 그래프를 그려보면 아래와 같다.

수학적으로는 윗부분이 대략 음(-)의 2차 함수형태이고, 통계학적으로는 정규분포와는 조금 다른 t분포의 모습을 보이고 있다. 어쨌든 이런 형태의 곡선은 거의 모든 시점에서 큰 오차를 보이지 않는, 어떤 함수형태로 그 값들을 추정해 낼 수가 있다.

단순득표수 그래프는, 정점에 이를 때까지 그 기울기가 지속적으로 증가하고 있다. 즉 항상 df/dt>0 인 것이다. 그리고 정점을 지나면 또 계속해서 그 기울기가 지속적으로 감소한다. 역시 언제나 df/dt<0 인 것이다.

왜 이렇게 되는가? 그것은 30분 간격의 단순 그래프의 변화가, 정점을 중심으로 해서, 좌우로 한 번도 굴곡을 나타내는 변화를 보이지 않기 때문이다. 그렇다면, 이런 모습을 보이는 것이 정말로 현실적인 것인지를 반문해 볼 필요가 있다.

개표 당시에 250여개의 개표소에서 개표가 동시에 진행되고 있었다. 어떤 개표소에서는 박근혜의 표가 많이 나올 수가 있다. 또 다른 개표소에서는 반대로 문재인의 표가 더 많이 나올 수 있다. 그러므로 이를 전국적으로 합산한 박근혜 후보의 득표수는, 이를 30분 간격으로 살펴볼 때, 어떤 시간에는 바로 그 직전 시간보다 더 많이 나올 수도 있지만, 또 어떤 시점에는 그 바로 직전 시간보다 더 적게 나올 수도 있다.

이런 변화가 꼭 정점을 중심으로 해서, 정점에 도달하기 전까지는 항상 그 직전보다 더 많이 나오고, 정점에 도달한 이후에는 반드시 그 직전보다 더 적게 나와야만 되는 것이 아니다. 이것은 자연스러운 모습이 아닌 것이다.

정점에 도달하기 이전에도, 바로 직전 시점보다 얼마든지 더 적게 나올 수도 있고, 또 그러다가 더 많이 나올 수도 있는 것이다. 마찬가지로, 정점에 도달한 이후에도 그 직전 시점보다 더 많이 나올 수도 있고, 또 얼마든지 더 적게 나올 수도 있는 것이다. 이것이 자연스러운 개표상태의 모습이다. 특히 두 후보의 대결이 박빙일 경우에는 더욱 더 그렇다.

개표가 이루어지고 있는 그 시점에서, 만약 30분간 문재인 후보의 득표수가 상대적으로 더 많았다면, 박근혜 후보의 득표수는 상대적으로 더 적어지게 될 것이고, 그 결과 박근혜 후보는 그 이전 30분에 득표했던 것보다도 더 적게 득표할 수 있는 것이다.

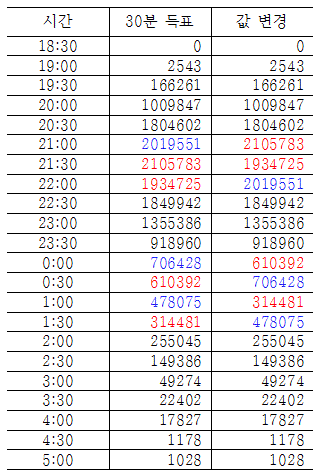
이제 이런 상황을, 표로 만들어서 살펴보기로 하자.

30분 간격의 단순 득표수 값이, 일부 구간에서 등락을 거듭하는 것을 알 수 있다. 이를 그래프로 그려보면 아주 분명하게 살펴볼 수 있다.

이런 형태의 그래프는, 큰 오차 없이 함수에 의한 추정치로 나타내기가 거의 불가능한 것이다. 왜냐하면 어떤 형태의 함수를 추정 모델로 만들더라도, 등락이 발생하는 부분에서는 갑자기 오차가 커질 수밖에 없기 때문이다.

이제 이런 30분 간격의 단순득표수를 가지고, 시점별로 변경된 누적득표수를 구해서 원래 값과 비교해보면 다음과 같다.

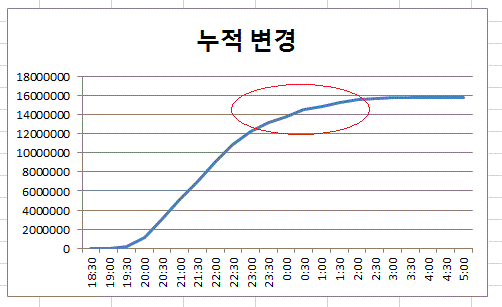
먼저 변경된 누적득표수를 그래프로 그려보면, 아래와 같이 된다. 30분 간격의 득표수가 등락을 보임으로 말미암아, 누적득표수를 나타내는 로지스틱 곡선 상에도, 붉은색 원으로 표시한 부분에, 매끄럽지 않은 굴곡이 생긴 것을 확인할 수 있다.

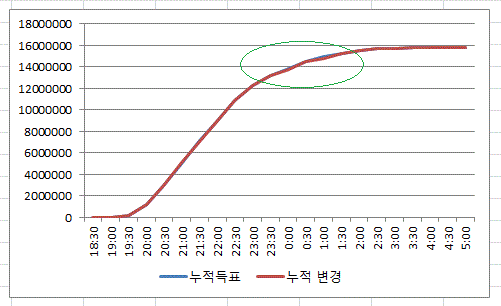
이를 다시 한 번 확인하기 위해서, 원래의 그래프와 함께 그려보기로 하자.

초록색 원 안의 부분이, 굴곡이 발생한 부분이다. 이런 굴곡으로 인해서 로지스틱 곡선은 매끄럽지 않게 되는 것이다. 만약 30분 간격의 득표수 값의 변화가 더 커지게 된다면, 이런 굴곡 현상은 더욱 더 뚜렷해지게 된다.

어떤 시점에서는, 문재인 후보의 표가 집중적으로 많이 나오고, 그에 따라 박근혜 후보의 표가 상대적으로 더 적게 나오는 때가 있을 것이다. 따라서 이때는 박근혜 후보의 득표수는 상대적으로 이전 시점보다 줄어들게 될 것이고, 반면에 문재인 후보의 득표수는 이전 시점보다 더 많아지게 될 것이다. 이것은 전체적인 득표수 규모가 증가하고 있는 상황에서도 역시 동일하게 발생될 수 있는 현상이다.

따라서 이런 경우에는 박근혜 후보의 누적득표수를 나타내는 그래프만 굴곡 현상을 나타내는 것이 아니라, 문재인 후보의 그래프도 역시 굴곡 현상을 나타내게 되어 있다. 비록, 전체적인 그래프가 아무리 로지스틱 곡선 형태를 띠고 있다고 하더라도 말이다.

하지만 SBS에서 발표한 박근혜와 문재인 두 후보의 로지스틱 곡선을 살펴보면, 이런 굴곡이 전혀 없이 아주 매끄럽고 나란히 진행되는 것을 발견하게 된다.

이는 이들 두 후보의 30분 단위의 단순득표수가, 전혀 등락이 없이 어떤 함수적인 형태의 모습을 보이면서, 그 값이 정점을 중심으로 일정한 방향으로만 변하고 있기 때문에 발생한 것이다. 이제 두 후보의 30분 단위 단순득표수 값을 살펴보면 아래 표와 같이 된다.

그리고 이 값들을 그래프로 그려보면, 아래와 같다.

문재인 후보의 경우에는, 박근혜 후보에 비해서, 정점 부근에서 조금 각진 모습을 보이고 있지만, 그럼에도 불구하고 그 증감의 방향이 정점을 중심으로 해서 변하지 않기 때문에, 누적득표수 그래프는 매끄럽게 나타나는 것이다.

그리고 두 후보 사이의 이런 30분 간격의 단순득표수 그래프도, 정점에 이르기 직전 한 시간(20;30~21:30) 만을 제외하고는, 거의 똑 같은 모습으로 움직이고 있다. 이것도 역시 조금 이상하게 생각된다.

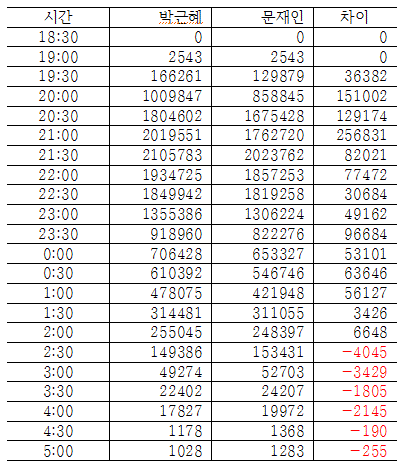
이제 두 후보의 30분 간격의 단순득표수 차이를 살펴보기로 하자.

이들 득표수 차이는, 개표가 거의 끝나갈 무렵인 새벽 2:30 이후를 제외하고는 항상 박근혜 후보의 득표수가 문재인 후보보다 더 많았다. 그리고 또 새벽 2:30 이후에는 항상 문재인 후보가 더 많은 것으로 나타나고 있다. 만약에 이번 대선이 진짜 박빙의 선거였다면, 어떻게 그런 박빙의 선거에서 이 같은 개표 결과가 나올 수가 있는가?

만약 개표조작이 전혀 없었다면, 거의 개표 예술과도 같은 것 아니겠는가? 아주 치밀하고 정교하게 맞추어, 250여개의 개표장에서 일사불란하게 개표를 진행해서 만들어 낸 행위 예술처럼 말이다.

지금까지 살펴본 것처럼, 굴곡이 거의 없는 매끄러운 로지스틱 곡선은, 교수들이 주장하는 것처럼, 분당 최대 득표수가 y축 값에 비해서 상대적으로 너무 작기 때문에, 매끈하게 나타난 것이 결코 아니다.

그래프가 매끈하게 나타난 것은, 그것과는 전혀 별개로 30분 간격의 단순득표수 증가가, 대체로 일정한 방향성을 띤 함수적인 모습으로 증가했기 때문에 발생한 것이다.

이상으로 저의 반론을 모두 마칩니다. 감사합니다.

 

 

시사인 기사에서 보도한 서울대 및 고려대 교수님의 해명에 대한

그루터기추억님의 최신반론입니다.