더플랜에 대해서 파파이스가 자료를 올렸습니다.

현화신, 전희경 씀.

<더 플랜>에서 제기한 K 값에 대한 관심에 감사드리며, 영화 상영 후 제기된 여러가지 의문들을 다섯가지 유형으로 묶어 보충 설명을 드리고자 합니다.

먼저, 아래에 있는 그래프가 K=1.5 를 (빨간색 선) 찾게된 계기였습니다 (adjusted R2=0.98). 회색 점선으로 나타낸 대각선이 K=1 일 때를 나타내는 것입니다. K>1 라는 것은 미분류표에서 분류표와 비교될때 후보1에게 상대적으로 더 많이 재분류되었던 어떤 이유가 있었다는 것을 의미합니다. 따라서 그 원인들을 찾기 위해 몇 가지 가설을 함께 논의하는 과정이 되기를 희망합니다.

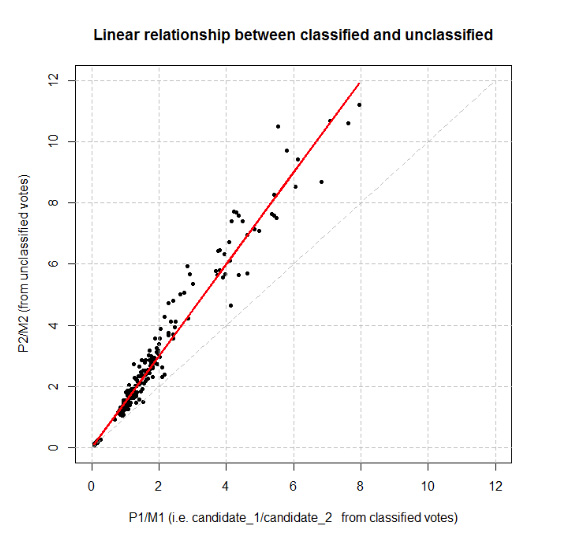
 P1 /M1 (x‐axis)= 분류표에서 (후보 1 의 표/후보 2 의 표)
 P2/M2 (y‐axis) = 미분류표에서 (후보 1 의 표/후보 2 의 표)
 (P2/M2)=K* (P1/M1), 빨간 선이 K=1.5 임을 보여주는 것임.

가설 1. 미분류표 비율이 높을수록 K‐값이 크다?

-> 아닙니다. 미분류표가 많을수록 K‐값이 커지지 않습니다. 왜냐하면 K‐값은 미분류표 뿐만 아니라 분류표까지 포함해서 나온 비율이기 때문입니다. 아래 그래프가 보여주듯이, 오히려 미분류율이 높은 지역에서는 K‐값이 작아지는 것으로 나왔습니다. (U_rate=미분류 비율)

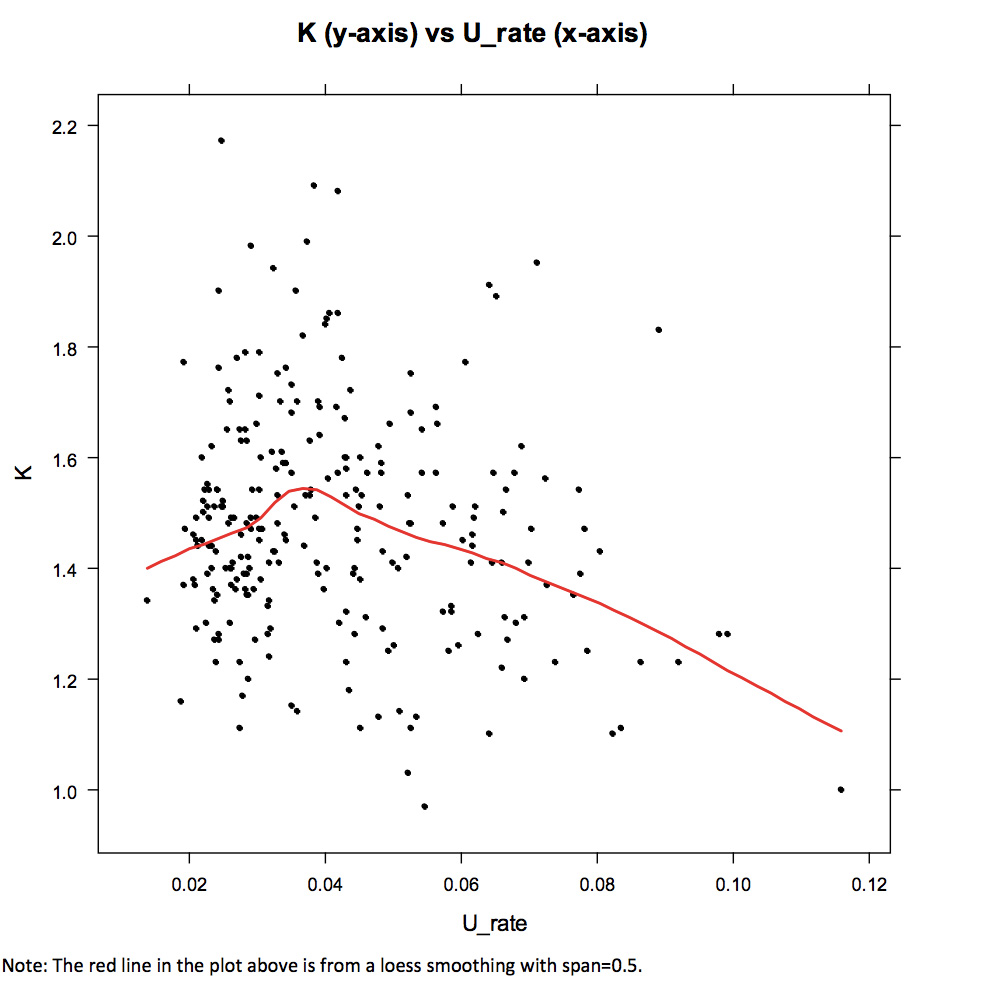
가설 2. 투표자 50 대 이상 비율이 높을수록 K‐값이 크다?

-> 아닙니다. 아래 그래프 (a)가 보여주듯이 K‐값은 50 대 이상 비율과는 거의 상관이 없습니다. 그래프 (b)는 노령층이 높으면 미분류율도 높아지는 것을 보여줍니다. 그러나 그래프 (c) & (d)는 노령층이 많은 지역에서 후보 1 과 후보 2 의 미분류 비율이 함께 높아지는 것을 보여줍니다. 따라서 노령층 비율이 커진다고 K‐값이 커지는 것은 아닌 것으로 드러났습니다. 왜냐하면 K‐값은 미분류표 뿐만 아니라 분류표까지 포함해서 나온 비율이기 때문입니다. (한국 통계청 전국 인구통계 자료 사용)

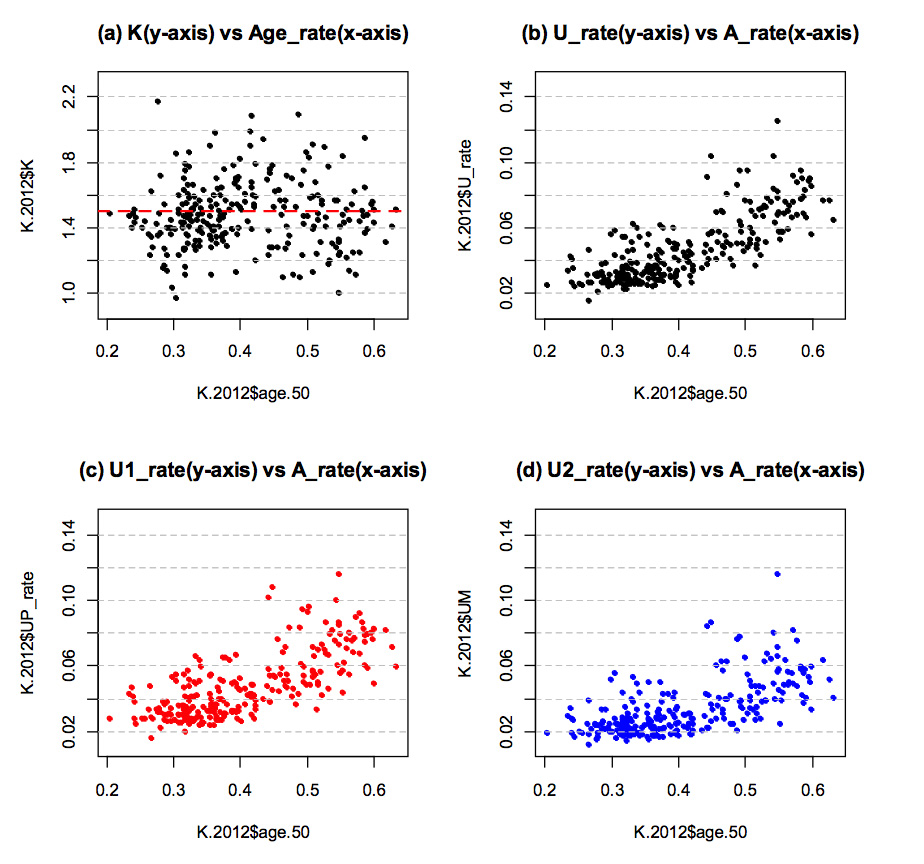
가설 3. 여성 비율이 높을수록 K‐값이 크다?

-> 아닙니다. 아래 그래프 (e)가 보여주듯이 K‐값은 여성 비율과는 상관이 없는 것으로 나타났습니다. 후보 1 이 여성들의 지지를 받은 것으로 알려져 있으나, 여성들의 비율이 높아서 K‐ 값이커지는것으로드러나지않았습니다. (한국통계청전국인구통계자료사용)

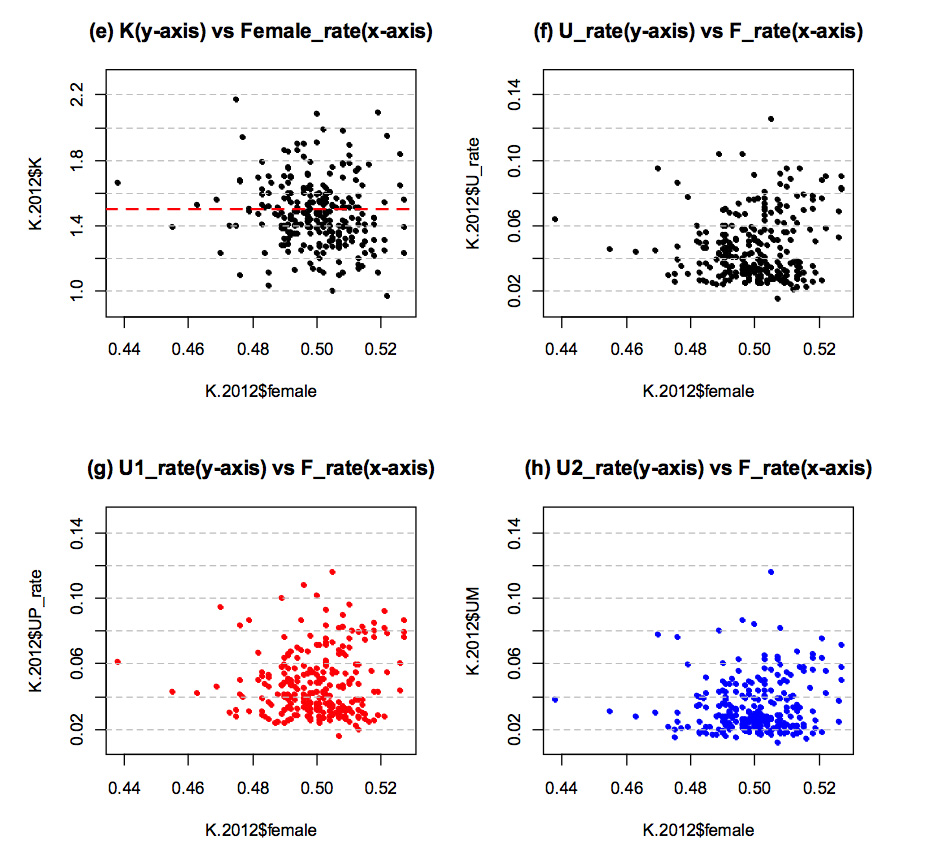
가설4.미분류표 비율에 있어서, 50대 이상 노령층에서만 후보1이 후보2보다 높다?

-> 아닙니다. 아래 그래프가 보여주듯이, 노령층뿐만 아니라 모든 연령층에서 후보 1 은 후보 2 보다 미분류 비율이 높게 나왔습니다. 예를 들어 50 대 이상이 20~40%인 상대적으로 젊은 지역에서도 후보 1 의 미분류율이 (빨간색 선) 후보 2 (파란색 선)보다 높게 나타났습니다. 달리 표현하자면, 모든 연령층에서 후보 1 투표지들이 더 많이 미분류되었다는 것입니다. 나이에 상관없이 후보 1 의 투표자들이 후보 2 투표자들보다 투표지에 도장을 전자개표기가 판독할 수 없는 상태로 더 많이 찍었다는 (미분류표의 정의) 것을 보여주는 것입니다. 왜 그럴까요? (아래 질문 참고)

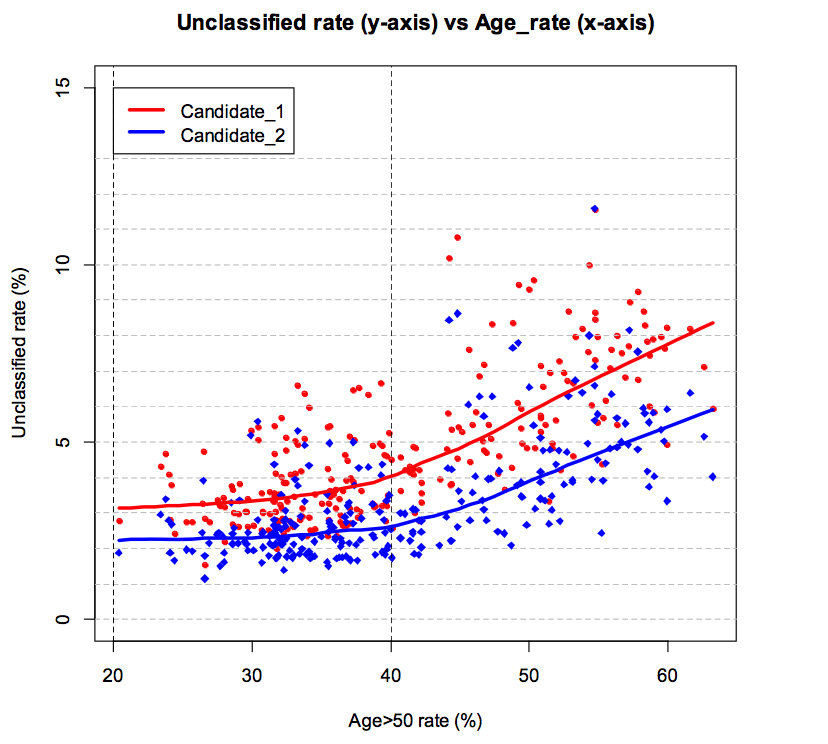
참고: 위 그래프는 가설 2 의 그래프 (c) & (d)를 합쳐 놓은 것으로 비율을 %로 표현한 것입니다.

가설 5. 미분류표 재검 기준에서 후보 1 과 후보 2 의 도장이 찍히는 넓이 비율에서 K‐값이 나온다?

(1) 먼저 미분류표 재검에서 후보1과 후보2의 도장이 찍히는 넓이가 다르다면, 한 후보에게 유리하고 다른 후보에게는 불리하므로 공정한 기준이 아닙니다. 이 부분은 사실 확인 후 개선되어야 할 부분입니다.
(2) 일단 18 대 대선에서 도장이 찍히는 넓이가 다르게 결정되었다고 가정하면, 그 넓이의 비율이 바로 미분류표 비율이 될 것으로 생각되지만 그렇지 않습니다. 왜냐하면 그 넓이의 밀도가 (도장 찍히는 빈도) 다르기 때문입니다. 아래에 있는 빨간색과 파란색 직사각형 내부에서 (가로=d & 높이는 각각 h1 & h2), 도장이 가장 많이 찍히는 부분이 그 안에 있는 작은 직사각형이라고 하고, 그 넓이를 S 라고 놓습니다.
(a) W1=작은 직사각형에 도장이 찍히는 빈도를 나타내는 비율, W2=나머지 넓이에 도장이 찍히는 비율. 여기에서 W2=1- W1 입니다. 예를 들어 서울역과 (W1) 그 주변 거리를 (W2) 사람들의 방문 빈도로 비교하시면 됩니다.
(b) 빨간색 후보 1 의 표로 인정되는 도장이 찍히는 넓이= W1* S+ W2*(d*h1- S)
(c) 파란색 후보 2 의 표로 인정되는 도장이 찍히는넓이= W1* S+ W2*(d*h2- S)
따라서 후보1과 후보2의 도장이 찍히는 넓이 비율은 h1/h2가 아니라 (b)/(c)가 됩니다. 이 값은 h1, h2, W1 & W2에 의해 결정되는데, 이에 대한 정보가 없으므로 식으로만 나타냅니다. 만약 W1>>> W2, (b)/(c) ≈ 1 에 가까워집니다.

질문: 미분류율에서 연령에 상관없이 후보 1 이 후보 2 보다 왜 항상 높을까요? 또한 이 것이 정상일까요? (가설 4 그래프 참고)

총 251 개표 지역 중에서 두 군데를 제외하고 나머지 249 지역에서 후보 1 의 미분류율이 후보 2 보다 높게 나왔습니다 (99%). 이러한 쏠림 현상이 통계적 분석을 하게 된 동기였습니다. 달리 말하자면, 모든 연령층에서 후보 1 을 지지한 투표자들은 후보 2 를 지지한 투표자들보다 더 많이 미분류표를 (전자개표기가 판독할 수 없는 표) 발생시켰습니다. 예를 들어, 같은 젊은 연령의 투표자들이 지지하는 후보에 따라 투표지에 도장 찍는 방법이 다르다는 것을 어떻게 설명할 수 있을지요?
좀더 알아보기 위하여 아래와 같이 식으로 나타냅니다. (아래 부록 참고)

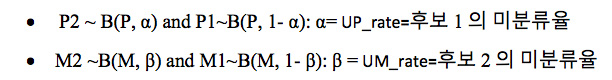
여기에서 α 와 β 는 개표 지역마다 다르지만, 앞에서 논의된 연령, 성별, 미분류표 재분류 기준, 또는알려지지 않은 다른 잠재적 원인 등등에 따라 달라지는 함수값이 되겠습니다. 두 후보간 상대적 비율인 K의 기대값을 α와β를 이용해서 나타내면 아래와 같이 표현할 수 있습니다.

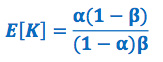
주의할 점은 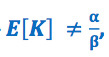, 즉 K는 두 후보의 미분류율의 비율과 같지 않다는 것입니다. 이부분이 잘못 이해되었기 때문에 앞에서 나왔던 가설들이 생긴 것이었습니다. 결국 미분류표 특성에 (profiles of unclassified votes of the two candidates) 대한 분석이 있어야 두 후보간 미분류율의 차이를 이해할 수 있겠습니다. 미분류표 특성에 대한 분석은 다음 선거에서 미분류를 방지할 수 있는 근거로 활용될 수 있고 개표를 개선시킬 수 있으므로 반드시 이에 대한 보고서가 필요하다고 판단합니다.

부록.jpg

알림: 현재 논문은 학회에서 발표되었지만, 저널에 게재된 상태가 아닌 working paper 입니다. 요청하는 분들이 있으나 논문 공유가 어려움에 대해 양해를 구합니다.

_______________________________________________________________________________________________________________________________

http://www.projectboo.com/archive/153353