작성자 : 설대원핵공
추천 : 13
조회수 : 1522회
댓글수 : 31개
등록시간 : 2014/07/01 19:11:08
| 옵션 |
|

위의 그림처럼 수도꼭지에서 졸졸 흐르는 물은 윗부분은 두꺼운 면적을 가지다가 점점 아래로 내려갈수록 얇아지는 모습을 취하게 됩니다. (물론 위의 그림에선 아랫부분에서 물이 모여있지만 그런 경우는 제외시킵시다.) 그럼 저 물줄기를 옆에서 바라보았을 때 나타나는 매끈한 곡선을 식으로 어떻게 나타낼 수 있을까요?

즉 이런 물줄기의 곡선을 수식으로 나타낼 수 있을까요?
그러기 위해서 우선 모든 유체는 어떤 부분에서든지 면적과 속력의 곱이 일정하다는 사실을 알고 있어야 합니다.

이런 통 안을 파란색 물이 흘러간다고 생각해봅시다. A 부분의 통 면적이 A, B부분의 통 면적이 B이며 A에서는 길이 s1만큼, B에서는 길이 s2만큼 흘러갔따면 , 같은 시간 t초 동안 저 부피만큼의 물은 항상 일정하게 유지되니까 A*s1이나 B*s2 나 같게 되죠. 이걸 시간 t로 나누면 결국 Av1=Bv2 라는 결론이 나옵니다. 즉 모든 유체는 모든 부분에서 면적과 속력의 곱이 항상 일정하게 나옵니다.
그럼 다시

이 곡선으로 돌아와봅시다. 편의상

반지름이 r인 수도꼭지에서 물이 초기속도 v0로 흘러나온다고 가정합시다. 물론 물은 +x 축 방향으로 중력을 받아 떨어지겠지요. 그리고 임의의 점 (x,y)의 관계를 알아보고자 합니다. x와 y의 관계를 바로 알 수는 없으니, 다른 변수를 이용하여 알아보는게 편할 듯 합니다. 그 때 사용하는 변수를 매개변수라 하며, 여기서는 시간으로 쓰는게 편하겠죠? 그래서 시간 t초가 지났다고 가정합시다.
그럼 등가속도 운동 식에 의해 저 점의 x좌표는
 가 되겠지요.
가 되겠지요.한편 (x,y)에서의 물의 속력을 구하려면 2as=v^2-v0^2 식을 이용하면

따라서 (면적)*(속력)=일정 의 사실을 이용하면
맨 처음 부분에서의 (면적)*(속력) 값은

즉 우리가 구하는 (x,y) 라는 점은 새로운 매개변수 t에 대하여
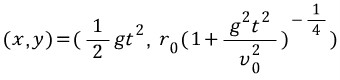 라는 식을 만족합니다.
라는 식을 만족합니다.
 식을 변형하면
식을 변형하면 이기 때문에 y에 대입하여 주면
이기 때문에 y에 대입하여 주면

2g/v0^2 은 일정한 상수 k 로 둔다면 중력에 의해 떨어지는 물줄기는 다음과 같이

r0=1, k=1 일 때의 그래프인


다음과 같은 물줄기 형태를 가진다는 사실을 알 수 있습니다. (x<0 인 부분은 무시하셔도 좋습니다. x>=0 이라는 자명한 조건을 달고 있기 때문에)
수도꼭지의 주둥이 반지름인 r0 가 넓어질수록 물줄기도 넓어질거란 사실은 자명합니다. 실제로

주둥이의 반지름을 2배로 넓히자 빨간색 그래프처럼 물줄기가 두꺼워지는 모습입니다.
그렇다면 k 값이 증가하면 어떻게 될까요? k=10 를 대입해보면(r0는 1로 고정)

빨간색 곡선처럼 더욱 홀쭉해진 모습을 볼 수 있습니다. k = 2g/v0^2 이니 k가 증가하려면 g가 증가하거나 v0 가 감소하여야 하죠. 즉 중력가속도가 더 크거나 물이 떨어지는 처음속도가 작으면 작을수록 물줄기가 더 빨리 홀쭉해진다는 사실을 알 수 있습니다.
봐주셔서 감사합니다.



