리만가설 소개에 관한 글입니다.
리만(Bernhard Riemann)은 1859년 한가지 추측을 했고, 이것을 현대에 리만가설이라고 부르고 있습니다. 이 가설에 내재된 여러가지 중요성이 있습니다만, 그 중 가장 주목받는 점 중 하나는 소수분포와 관련이 있다는 것입니다.
소수 분포를 알아내기 위해 다음과 같이 간단한 함수를 하나 정의하겠습니다.
즉 정수집합에서 자연수집합으로 가는 함수 π는, n보다 작은 소수들의 개수를 뱉어내는 함수입니다.
따라서 π가 어떻게 생겼는지를 알아내는 것이 곧 소수분포를 알아내는 것이 되겠습니다.
한편 "Prime number theorem(소수정리)"이라고 부르는 오래된 정리가 있습니다. π의 형태에 관한 정리입니다. 이 정리는 후에 몇 번의 refinement를 거쳤는데, 가장 유용한 버전은 아래와 같습니다.
이제  라고 편의상 줄여 쓰겠습니다. 그리고 위의 식을, 아래와 같이 간편히 쓰기도 합니다.
라고 편의상 줄여 쓰겠습니다. 그리고 위의 식을, 아래와 같이 간편히 쓰기도 합니다.
Prime number theorem : 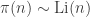 (Hadamard & de la Vallee Poussin(1896))
(Hadamard & de la Vallee Poussin(1896))
즉 소수 개수가 증가하는 속도와, 다소 "예쁘게 생긴 함수" Li가 증가하는 속도가 비슷하다는 것입니다.
한편 아래와 같은 사실은 고등학교 수학에서 잘 알려진 사실입니다.
따라서 π가 증가하는 속도 자체보다도, 이제 Li가 π를 "얼마나 잘 근사하는지" 궁금해 하는 것은 자연스러운 물음이 됩니다. 몇몇 수학자들은 π(n)-Li(n)에 대해 조사하기 시작했습니다.
이제 서술의 편의를 위해, 약간의 간단한 계산을 거쳐 Prime number theorem을 아래와 같이 변형하겠습니다.
(여기서  이고 2nd Chebyshev function라고 부릅니다.)
이고 2nd Chebyshev function라고 부릅니다.)
π(n)-Li(n) 대신 ψ(n) - n을 살펴보아도 되겠습니다.
■ ψ(n) - n 에 대해 알려진 것들
■ Riemann hypothesis : 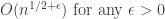 (the best of the best error term)
(the best of the best error term)
결국 '리만가설'이란, "예쁜함수(Li)"가 소수분포를 얼마나 잘 보여주느냐에 대한 것입니다.
사실, 리만가설은 리만제타함수(Riemann zeta function)으로 대중에게 더 잘 소개되고, Riemann의 original paper에도 그렇습니다.
일반적인 Riemann zeta function의 construction은 아래와 같습니다.
ζ : C(the set of complex numbers) → C
1) s∈C with Re(s)>1에 대하여,  라고 정의한다.
라고 정의한다.
2) Otherwise, 위 ζ의 analytic continuation을 생각한다.
이러면 ζ는 s≠1에 대해 잘 정의되는, C 위의 (meromorphic) function임을 확인할 수 있습니다.
ζ(s) = 0이 되는 s를 "ζ의 zero"라고 부릅니다. 비교적 어렵지 않은 계산을 통해, s=-2, -4, -6, ...이 ζ의 zero임을 알 수 있습니다.
이 negative even을 ζ의 trivial zero라고 부릅니다.
한편 ζ는 위의 negative even 말고도 무수히 많은 다른 zero들을 가지는데, 이를 ζ의 nontrivial zero라고 합니다.
이 nontrivial zero들은 전부(!) 0<Re(s)<1(called 'critical strip')에 깔려있으며 Re(s)=1/2와 Im(s)=0에 대칭임이 알려져있습니다.
아래 그림을 보시면 이해가 쉬우실 겁니다.
한편 저 nontrivial zero s들이 ![\displaystyle \textrm{Re}(s) \in \Biggl[ \frac{1}{2}-a, \frac{1}{2}+a \Biggr] \displaystyle \textrm{Re}(s) \in \Biggl[ \frac{1}{2}-a, \frac{1}{2}+a \Biggr]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Ctextrm%7BRe%7D%28s%29+%5Cin+%5CBiggl%5B+%5Cfrac%7B1%7D%7B2%7D-a%2C+%5Cfrac%7B1%7D%7B2%7D%2Ba+%5CBiggr%5D+&bg=ffffff&fg=333333&s=0) 에만 깔려있다면(즉 더 좁은 strip에만 있다면),
에만 깔려있다면(즉 더 좁은 strip에만 있다면),
아까의 Li(n)의 approximation이 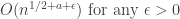 이라는, 다소 충격적인 사실이 또한 알려져있습니다.
이라는, 다소 충격적인 사실이 또한 알려져있습니다.
간단히 말해, 저 점들이 "좁게" 분포하면 분포할수록 Li는 소수 분포를 더 잘 근사한다는 것입니다.
저 점들을 가장 좁게 분포시키려면...
■ Riemann hypothesis (the original) : ζ의 nontrivial zero는 전부(!) Re(s)=1/2에 깔려있다.
이러한 sense에서, 리만가설은 Li의 square root error가 best라고 말할 수 있겠습니다.
아래는 리만가설 관련한 몇가지 어그로에 대한 답입니다.
1. ζ와 π가 대체 어떻게 connect되어있는지?
: Euler product라고 불리우는 을 이용하면, ζ와 prime number가 연관되고, further calculation을 통해 prime number theorem과 연관시킬 수 있음.
을 이용하면, ζ와 prime number가 연관되고, further calculation을 통해 prime number theorem과 연관시킬 수 있음.
: Euler product라고 불리우는
2.  ???
???
: 중간의 무한급수 표현은 통상 쓰는 partial sum의 limit이 아님. Riemann zeta function 정의를 고려할 때, analytic continuation으로 확장한 domain에서도 이러한 더하기 표기 하면 멋있으니 그냥 차용해서 쓴 것임.
: 중간의 무한급수 표현은 통상 쓰는 partial sum의 limit이 아님. Riemann zeta function 정의를 고려할 때, analytic continuation으로 확장한 domain에서도 이러한 더하기 표기 하면 멋있으니 그냥 차용해서 쓴 것임.
3. 리만가설이 풀리면 현대 암호체계 폭망?
: O(x^(1/2))라고 망하진 않는다고 생각함. 이에 대해서는 자세히 공부 안해봐서 정확한 이유는 모르겠음...
리만가설을 푸는 것에서 얻는 것은 mathematical beauty 및 증명에 쓰인 아이디어와 통찰력이라고 생각함.
4. 아티야가 푼게 맞냐?
: 아닐 가능성이 매우매우매우 높음.
: 아닐 가능성이 매우매우매우 높음.
5. 지금까지 증거가 없으면 귀납적?으로 거의 리만가설 맞다고 볼 수 있냐
: 리만가설과 상당히 관련이 있는, "거의 맞지만 아닌" 예를 아래 소개하겠음.
: 리만가설과 상당히 관련이 있는, "거의 맞지만 아닌" 예를 아래 소개하겠음.
위의 논의에서 π를 Li가 근사한다고 했는데, 그 그래프는 아래와 같음.
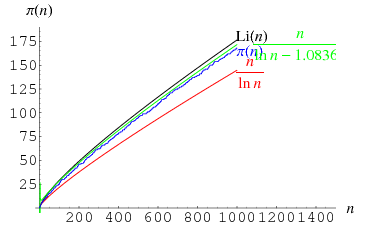
위의 그래프에서 검은선(=Li)이 파란선(=π)보다 항상 위에 있는가? 즉 항상 Li > π인가?
이에 대해 몇가지 알려진 사실은,
1) Li(n) < π(n) 인 n은 무수히 많음 (1914, John Edensor Littlewood)
2) Li(n) < π(n) 인 n은 10^(10^(10^964)) 이하에는 존재함 (1955, Stanley Skewes)
(이 사람의 이름을 따 Li(n) < π(n)인 n을 Skewes number라고 부름)
2') Li(n) < π(n)인 n은 1.39716 x 10^316 이하에는 존재함 (2011, Stoll & Demichel)
3) 컴퓨터로 2015년까지 노가다 해보니 n=1~10^19에 대해 Li(n) > π(n)
존재성은 증명이 되는데 대체 어디있는지 아직도 못찾았음...



 글쓰기
글쓰기