몇번의 글을 써본 결과, 글 내용이 복잡해질 수록 추천이 별로 없는거 같아요ㅠ.ㅠ
그래서 오늘은 간략히 수학과 예술의 만남! 프랙탈(fractal)도형에 관해 쓰…려고 하였으나 그 마저도 내용이 복잡하게 전개될 거 같아 오늘은 그 중에서도 굉장히 유명한!! 프랙탈이라는 이름을 만든 故 Benoit B. Mandelbrot翁(2010.10.14 사망)을 기려 만델브로 집합(Mandelbrot set)을 소개하려고 합니다. 오늘도 베오베에 한번 도전!
여러분은 고등학교 때 배운 점화식을 기억하시나요? 수열에서, 전 항(들)의 관계로부터 뒷 항을 만들어내는 식을 점화식이라고 합니다. 예를들어 등차수열 의 경우,
(단,
는 상수)가 됩니다. 여기에 초기조건
값만 주어지면 수열이 점화식으로부터 전부 쏟아져나오겠죠.
만델브로 집합 또한 복소수 수열 에 대한 간단한 점화식 관계로부터 도출됩니다.
(단,
는 상수)라는 점화식을 생각하고, 첫항을
라 합시다. 그러면 이 수열은 전부 결정되는데, 이 때 모든 항(복소수)의 크기(실수부와 허수부의 제곱의→합의→양의 제곱근)가 어떤 유한범위 내에 갇혀있으면 그에 해당하는
를 집합
안에 집어넣습니다. 이렇게 전~부 집어넣은
을 바로 만델브로 집합이라고 합니다.
예를들어, 로 두면,
과 같이 수열의 크기가 계속 크기가 커짐을 알 수 있습니다. 따라서
은
에 들어가지 않게 됩니다.
반면 로 두면,
과 같이 수열의 크기가
를 넘어가지 못함을 알 수 있고,
는
에 들어가게 됩니다.
(Mandelbrot set 의 정의를 Formal하게 다시 적으면,
There exists a constant
such that for any
)
의 영역을 복소평면위에 검게 칠하면 다음과 같은 그림이 됩니다.
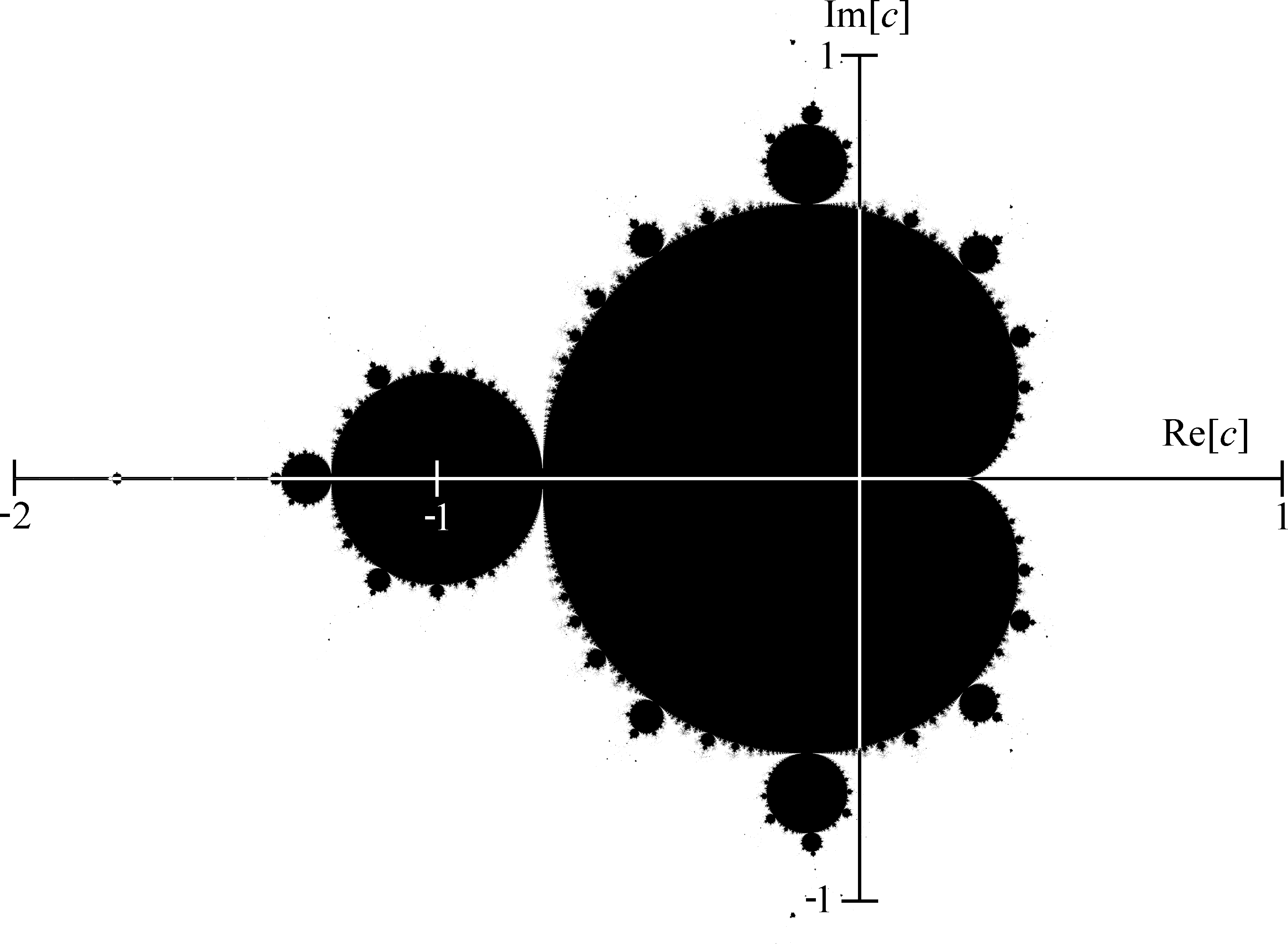
[만델브로 집합(Mandelbrot set)]
무슨 외계 생명체같이 생겼네요… 뻗어나가는 세균같기도 하고…-_-a
조금 더 퐌타스틱하게 보이기 위해 색을 좀 칠하면 다음과 같은 알흠다운 그림이 얻어집니다.

(색을 칠하는 방법에는 여러가지가 있습니다만, 대부분 (아까 말씀드린 수열의 크기)가 무한대로 접근하는 속도에 따라 다른 색을 칠하는 방식을 씁니다.)
그렇다면 만델브로가 프랙탈인가? 그러고보니 프랙탈 도형의 소개를 안했네요. 아주 rough하게 말하자면, 프랙탈 도형이란 자기유사성(self-similarity)을 가지고 있는 도형이라고 정의합니다. 자기유사성이랑 어떤 부분을 적당히 확대 시켰을 때 다시 같은 패턴이 나오는 것을 뜻하는데, 예를 들면 다음과 같은 도형들입니다.

[코흐의 눈송이(Koch snowflake)]

[멩거 스폰지(Menger sponge)]
이것들은 인간에게 신비감을 주기 때문에 예술 작품의 아이디어가 되기도 하며, 이러한 예술을 프랙탈 예술(Fractal art)라고 합니다.
그렇다면 만델브로 집합은 어떤 자기유사성을 가지고 있을까요? 안타깝게도, 만델브로 집합이 자기유사성을 띄는 부분은 그렇게 많지 않습니다. 하지만 확대시켰을 경우, 완전히 자신와 같지는 않더라도 “거의 같은” 경우는 많고, 또한 아무리 확대 시켜도 “복잡성”을 유지한다는 것이 특징입니다. 예를들어 원의 한 부분을 확대 시키면 보다 단순한 도형 직선에 가까워지지만, 만델브로 집합은 그러한 현상을 보이지 않습니다.
(여기서 “거의 같은”과 “복잡성”은 수학적으로 엄밀하게 정의될 수 있으나 생략하겠습니다.)

[만델브로 집합의 자기 유사성]
위의 이미지를 보시면 처음 그림과 완전히 같아지는 그림처럼 보이는 경우가 몇번 있을텐데, 사실은 그게 완벽하게 똑같지는 않습니다(꼬리 부분의 구성이 조금 다르게 됩니다.). 이러한 자기 유사성을 quasi-self-similarity라고 합니다.
이 이상 얘기하면 머리아파지니까 그만하고, 그렇다면 오늘의 하일라이트!!!!
만델브로 집합을 지대로 여행해 볼까요?^^*
수학으로 베오베 가는 그날까지!!
읽어주셔서 감사합니다(__)


 글쓰기
글쓰기